is guaranteed to converge ifDepartmental Final Exam
2 pts 1. The series
is guaranteed to converge if
a) the sequence 
converges b) 
for some constant
L < 1
c) 
d) 
e) 
f) 
g) for all 
and 
, for some r such
that 0 ? r < 1.
h) none of the above is enough to guarantee that the series converges
i) any of the conditions (a)-(g) is enough to guarantee that the series converges
1pt ea. 2&3. Fill in the blanks in the following statement to make it correct. The expression
you put in the first blank will be your answer to (2), and the expression you put in
the second blank will be your answer to (3):
"We say 
if and only if for every e
> 0, there is a positive integer k such
that whenever ."
a) 
b) 
c) 
d) 
e) 
f) 
g) n > k h) k > n i) n > e
j) k > e
2 pts 4. The improper integral 
diverges if and only if
a) p < 1 b) p ? 1 c) p ? 1
d) p > 1 e) p ? 2
In problems (5)-(9), assume that ƒ and g are continuous functions on [a,b] with ƒ(x) ? g(x) ? 0, and assume that the derivative of ƒ is also continuous on [a,b]. Choose from the following list, the correct formula for the stated task:
a) 
b) 
c) 
d) 
e) 
f) 
g) 
h) 
i) 
j) none of these
2 pts 5. To find the volume of the solid generated by revolving about the x-axis the region between the graph of y = ƒ(x) and the x-axis, for x in [a,b].
2 pts 6. To find the area of the surface generated by revolving about the x-axis the graph of y = ƒ(x), for x in [a,b].
2 pts 7. To find the length of the curve formed by the graph of y = ƒ(x), for x in [a,b].
2 pts 8. To find the volume of the solid generated by revolving about the y-axis the region between the graph of y = ƒ(x) and the x-axis, for x in [a,b].
2 pts 9. To find the volume of the solid generated by revolving about the x-axis the region between the graphs of ƒ(x) and g(x), for x in [a,b].
Problems (10) and (11) have the same set of choices.
a) cos y b) x cos y + sin y c) sin y
d) x cos y e) x + sin y f) 1
g) 1 + cos y h) –x cos y
2 pts 10. If ƒ(x,y) = x
sin y, what is 
?
2 pts 11. If ƒ(x,y) = x
sin y, what is 
?
4 pts ea 12. Compute the following four integrals:
i) 
ii) 
iii) 
iv) 
3 pts ea 13. Determine whether the following three series converge or diverge. Justify your
answers (e.g., by citing an appropriate convergence test).
i) 
ii) 
iii) 
6 pts 14. For which real numbers
x does the power series 
converge?
6 pts 15. Find the fifth degree Taylor
polynomial 
of 
about 0 and use it to
estimate 
.
6 pts 16. Graph 
in polar coordinates. Set up, but do not evaluate, an integral (or
sum of integrals) representing the area of the region enclosed by this curve.
6 pts 17. Find the arclength of the graph of y = ln(sec x), 0 ? x ? p/4.
8 pts 18. Let
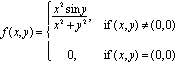
a) Find 
and 
.
b) Find the directional derivative of ƒ at the origin in the direction of the
vector 
.
6 pts 19. Compute 
.
You may consider interchanging the order of
integration.
8 pts 20. The function ƒ is positive, increasing, and concave downward on the interval [a,b].
The integral
is estimated using various methods, all with the same number of subintervals: the left-hand sum is L, the right-hand sum is R, the trapezoidal rule estimate is T, and the midpoint sum is M. Arrange the numbers L, R, T, M, and I in order from smallest to largest.
9 pts 21. Find the area A,
and the centroid or center of mass 
of the plane region
bounded above by the line y
= x+ 2 and bounded below by the parabola 