1. Label currents on wires using arrows.

A) Direction doesn't matter, but must be consistent.

B) Current is the same between intersections.

2. Write down 'junction equations'.

A) Count the number of intersections. You will need one less equation than there are junctions.

B) Current is conserved at junctions. I in = I out.

3. Write enough loop equations to make up the necessary number to solve the system.

A) The change in energy, and thus the total voltage drop, around any closed path is zero.

B)Crossing a resistor with the current causes a -IR voltage. (Against the current, +IR)

C) Crossing a battery from - to + gives a +V, (+ to - gives a -V)

D) Be clever in your choice of loops.
 

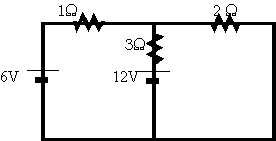
Example:
 
 
 
 
 
 
 
 
 
 
 
 
 

Especially useful for circuits where there are multiple batteries, and circuits where it is impossible to identify a circuit element as 'series' or 'parallel'.
 
 
 

R-C Circuits. (Contain both resistors and capacitors)
 

A capacitor is, in effect, a break in the circuit. When the capacitor is fully charged, no current will flow. It takes some time for the capacitor to charge, the amount of time depends on the resistance and capacitance. (Solve dq/dt= V/R -q/(RC) ->q=q₀ [ 1 -- e^-t/RC])